
自古以来,人类一直试图揭示宇宙的奥秘,用数学和科学的语言探索自然的规律。正如古希腊哲学家亚里士多德所言:“知识本身就是力量。” 这17个方程式不仅仅是抽象的数学表达式,它们如同钥匙,帮助我们解锁了世界的运转法则。从描述几何关系的毕达哥拉斯定理,到量子力学的薛定谔方程,这些方程式在科学史上刻下了不朽的印记。它们不仅改变了我们对自然的认知,也推动了科技的飞速发展。今天,与AJE一同回顾这些方程式的历史与意义,感受它们背后所蕴藏的科学之美与人类智慧的光辉。
1. 毕达哥拉斯定理(Pythagoras's Theorem)
毕达哥拉斯定理 a^2 + b^2 = c^2是古希腊数学家毕达哥拉斯(Pythagoras)在公元前530年提出的,它描述了直角三角形三边之间的关系:在一个直角三角形中,直角两边的平方和等于斜边的平方。尽管这一定理在毕达哥拉斯之前可能已经被其他文化所使用,但毕达哥拉斯将其系统化,使其成为几何学中的核心内容。这一定理为后来的建筑学、制图学提供了坚实的数学基础,同时也是学习三角学的第一步,广泛应用于测量、工程等领域。
2. 对数(Logarithms)
对数方程log xy = log x + log y 于1610年由苏格兰数学家约翰·纳皮尔(John Napier)提出。对数将乘法和除法运算转换为加法和减法,使得复杂计算变得更加简便。在计算机和电子计算器诞生之前,天文学家、工程师和数学家依赖对数表进行繁复的运算。对数不仅极大地简化了计算过程,还奠定了指数和对数函数的基础,广泛用于各类科学分析中。
3. 微积分(Calculus)
微积分的基本公式之一是导数的定义

,由艾萨克·牛顿(Isaac Newton)和戈特弗里德·莱布尼茨(Gottfried Leibniz)在17世纪独立发展出来。微积分是研究变化和运动的数学工具,广泛应用于物理学、工程学、生物学等领域。通过微积分,人们得以解析复杂的运动轨迹、计算物体受力情况和预测系统变化。这一数学工具为科学革命提供了基础,被誉为“变化的数学”。
4. 万有引力定律(Law of Gravity)
万有引力定律
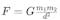
是牛顿在1687年发表的,描述了任意两质量物体之间的引力作用。通过这一公式,牛顿成功解释了行星轨道的运动、潮汐现象以及物体在地球上的自由下落。万有引力定律奠定了经典物理学的基石,不仅为天文学的发展提供了理论支持,还在工程、导航等应用中至关重要。
5. 负一的平方根(The Square Root of Minus One)
复数单位i^2 = -1 是数学家莱昂哈德·欧拉(Leonhard Euler)在1750年提出的,它引入了虚数的概念。虚数的引入扩展了数的定义,使得许多复杂的问题能够得到解答。现代工程学、物理学和电子学中,复数广泛用于信号处理、电流计算等领域,为我们理解和设计复杂系统提供了新的数学工具。
6. 欧拉多面体公式(Euler's Formula for Polyhedra)
欧拉多面体公式V - E + F = 2 于1750年由欧拉提出,描述了三维空间中多面体的顶点(V)、边(E)和面(F)之间的关系。这一公式揭示了几何学中的基本性质,为拓扑学的发展提供了基础。欧拉公式不仅在几何学中具有深远影响,还被用于化学和分子结构的研究。
7. 正态分布(Normal Distribution)
正态分布函数
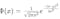
是高斯(Carl Friedrich Gauss)在1810年提出的,它描述了许多自然现象中的数值分布,如身高、体重、测量误差等。正态分布在统计学和概率论中具有核心地位,广泛用于数据分析、质量控制和风险评估中。
8. 波动方程(Wave Equation)
波动方程
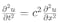
由达朗贝尔(Jean le Rond d'Alembert)在1746年提出,描述了波的传播特性。这一方程广泛应用于声学、光学、电磁学等领域,帮助人们理解和分析波动现象,如声音的传播、光的折射和电磁波的传输。
9. 傅里叶变换(Fourier Transform)
傅里叶变换

是由约瑟夫·傅里叶(Joseph Fourier)在1822年提出的,它将信号从时域转换到频域,使得复杂的周期信号可以被分解和分析。傅里叶变换在信号处理、图像处理和量子力学中具有广泛应用。
10. 纳维-斯托克斯方程(Navier-Stokes Equations)
纳维-斯托克斯方程

是由纳维(Claude-Louis Navier)和斯托克斯(George Stokes)在19世纪提出的,用于描述流体的运动。该方程是流体力学的核心,广泛用于航空、气象、海洋等科学领域,对流体模拟和预测起到了至关重要的作用。
11. 麦克斯韦方程组(Maxwell's Equations)
麦克斯韦方程组揭示了电磁场的本质,将电与磁统一成一个完整的理论。詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)于1865年提出的这四个方程,为现代无线电、通信和电子学奠定了理论基础。麦克斯韦方程组开创了电磁波研究的新时代,极大地推动了科技进步。
12. 热力学第二定律(Second Law of Thermodynamics)
热力学第二定律
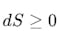
是鲁道夫·克劳修斯(Rudolf Clausius)和路德维希·玻尔兹曼(Ludwig Boltzmann)在19世纪提出的,指出了热量从高温传向低温的不可逆过程。该定律揭示了自然过程的方向性,为理解和控制热力学系统提供了基础。
13.玻尔兹曼方程(Boltzmann's Equation)
玻尔兹曼方程
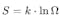
由奥地利物理学家路德维希·玻尔兹曼(Ludwig Boltzmann)于19世纪提出,用于描述热力学系统的熵(S)与微观状态数Omega之间的关系。该方程标志着统计力学的建立,为我们理解宏观系统的无序程度和自发性提供了理论支持。玻尔兹曼方程在物理学中具有基础性地位,是研究热力学过程、物质分布的重要工具。
14. 相对论质能方程(Einstein's Mass-Energy Equivalence)
爱因斯坦的质能方程E = mc^2 于1905年提出,是狭义相对论中的一个核心公式,表明质量(m)和能量(E)可以相互转换,其中 \( c \) 是光速。这个公式揭示了质量和能量的内在联系,是核物理学的基础,解释了核反应中所释放的巨大能量。质能方程不仅在理论上具有革命性意义,而且在核能、核武器等应用领域也产生了深远影响。
15. 薛定谔方程(Schrödinger's Equation)
薛定谔方程
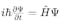
是量子力学的基础方程,由奥地利物理学家埃尔温·薛定谔(Erwin Schrödinger)于1925年提出。该方程描述了量子系统的波函数随时间的演化。薛定谔方程帮助我们理解亚原子粒子的行为和特性,为现代物理学中的微观研究提供了理论基础,在量子计算、半导体等技术中具有广泛应用。
16. 信息熵(Information Entropy)
信息熵公式

由信息理论之父克劳德·香农(Claude Shannon)在1948年提出,用于描述信息的不确定性。信息熵量化了数据传输过程中的信息量,为通信技术、数据压缩、密码学等领域提供了基础理论。香农的信息熵公式是现代信息论的基石,被广泛应用于计算机科学和通信工程中。
17. 黑洞熵公式(Black Hole Entropy)
斯蒂芬·霍金(Stephen Hawking)于1974年提出的黑洞熵公式
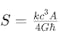
描述了黑洞的熵(S)与其表面积(A)之间的关系,这一公式将量子力学、广义相对论和热力学结合在一起,揭示了黑洞的热力性质。黑洞熵公式是研究宇宙学和量子引力的重要工具,有助于人们理解宇宙的基本结构和黑洞的性质。
最后
这17个方程式,是人类智慧的丰碑,承载着无数科学家在漫长岁月中不懈求索的成果。每一个方程式背后,都有一段科学史上的传奇故事,也有一位又一位敢于突破边界的探索者。他们在自己的时代留下了超越时空的洞见,而这些洞见不断激励着我们向未知领域进发。
今天,这些方程式已不仅仅是科学家的工具,它们在生活的方方面面为我们提供了无数便利。它们指引着航天器在浩瀚的星海中导航,让我们窥见微观世界的奇妙规律,甚至帮助我们预测未来的变化。无论是我们脚下的地球,还是遥远的宇宙,这些方程式的力量无处不在。
正如爱因斯坦曾说过的那样:“科学没有国界,因为它属于全人类。” 这些方程式正是科学共同体献给世界的无价之宝。它们跨越了语言、文化和地域的障碍,为所有热爱真理的人们搭建了一座通往知识的桥梁。展望未来,我们可以相信,新的方程式还会继续诞生,新的知识还会被发现。而这些过去的经典,将永远陪伴我们,指引着人类向更深邃的真理迈进,照亮我们前行的道路。
